By Michael Mampusti
Walk into a bathroom or kitchen and chances are that the walls or the floor are covered in square tiles. Perhaps not surprisingly, these collections of tiles are examples of tilings. The idea is that you are given a set of shapes, called tiles, and you cover an area, say your floor, with these tiles. You need to be careful, however. You must make sure that there are no gaps between tiles, that is, your tiling covers the whole floor. Furthermore, you can’t have tiles overlapping each other. If your tiled floor had gaps or bits of tiles protruding from the floor, you wouldn’t be a very happy chap.
Tilings of the plane are very similar to tilings of a bathroom floor, except this time, the floor has no boundary. Imagine you are standing on this floor, no matter how far you walk or run you never hit a wall. What you see in all directions is floor covered with tiles. To cover an area such as this, we require an infinite amount of tiles. These are tilings of the plane.
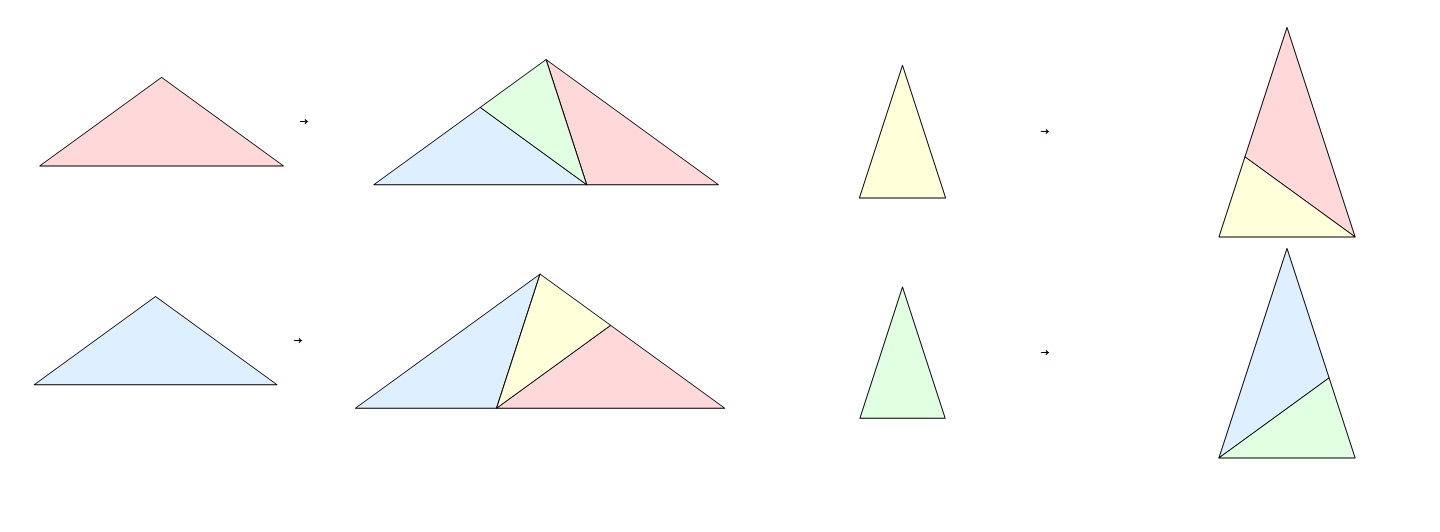
An important class of tilings of the plane are substitution tilings. These are tilings which cover the plane using substitution rules. Substitution rules are a combination of two things; inflation and subdivision. To illustrate this, let us consider the Penrose tiling. This is a tiling of the plane using four different triangles; red, blue, yellow and green. On each of these triangles, we define a substitution rule as follows.
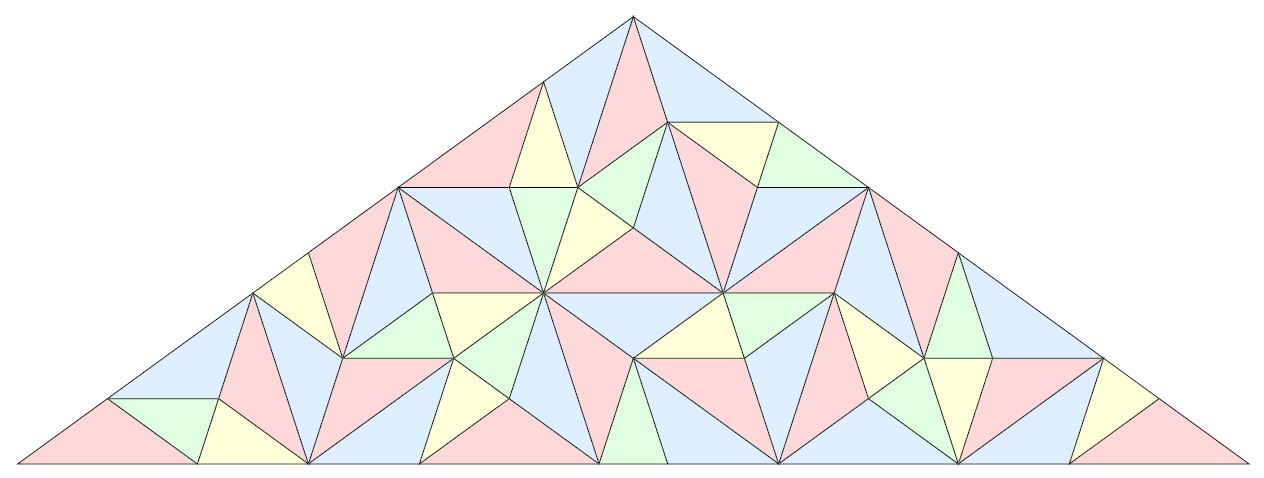
Each triangle is inflated and then subdivided so that they are made up of some combination of the four different triangles. For example, the red tile is inflated and subdivided into a blue, green and red tile. Now, taking the red tile and applying the substitution rules four times we obtain the following.
Applying the substitution rules indefinitely gives us a tiling of the plane. Pretty neat, huh?
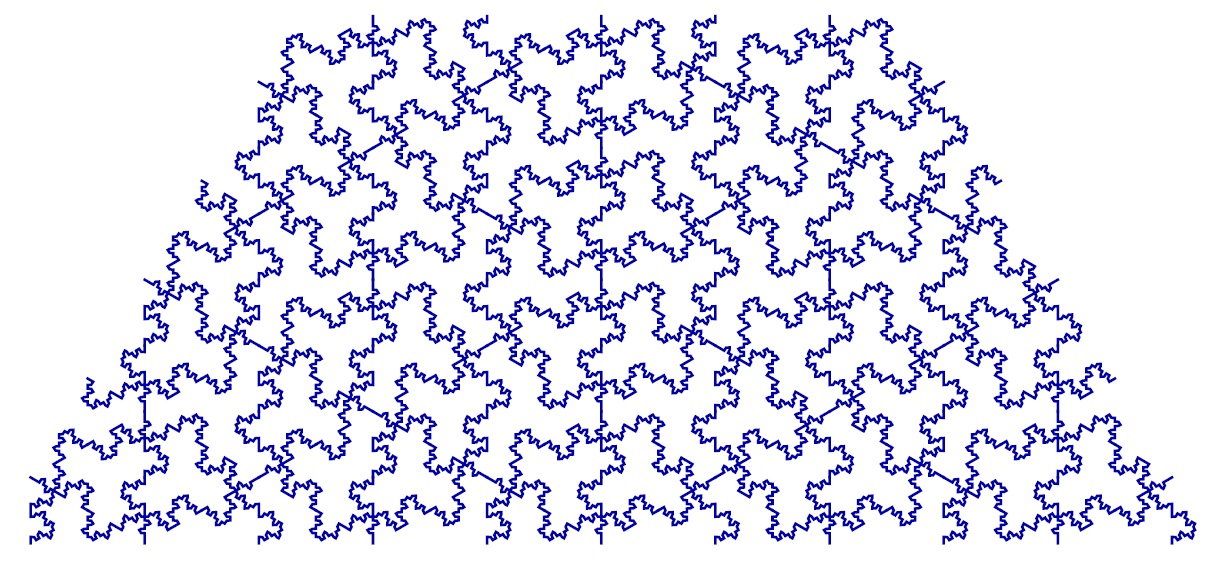
To make things even more interesting, we consider tilings of the plane with shapes that have fractal edges. Visually, this means that the boundary of each shape is super bumpy. We call these radical shapes fractiles. These tilings are fractal tilings of the plane.
In this project, we created a program which would produce fractal tilings of the plane through Wolfram Mathematica. The fractal tilings that we are able to create are actually built from already existing substitution tilings, such as the Penrose tiling. The substitution tilings we worked with also had an interesting property called aperiodicity. It turns out that examples of aperiodic tilings are hard to come up with. Our program is able to generate an infinite number of aperiodic tilings which are also fractal tilings!
Michael Mampusti was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.