By Justin Smallwood, The University of Melbourne
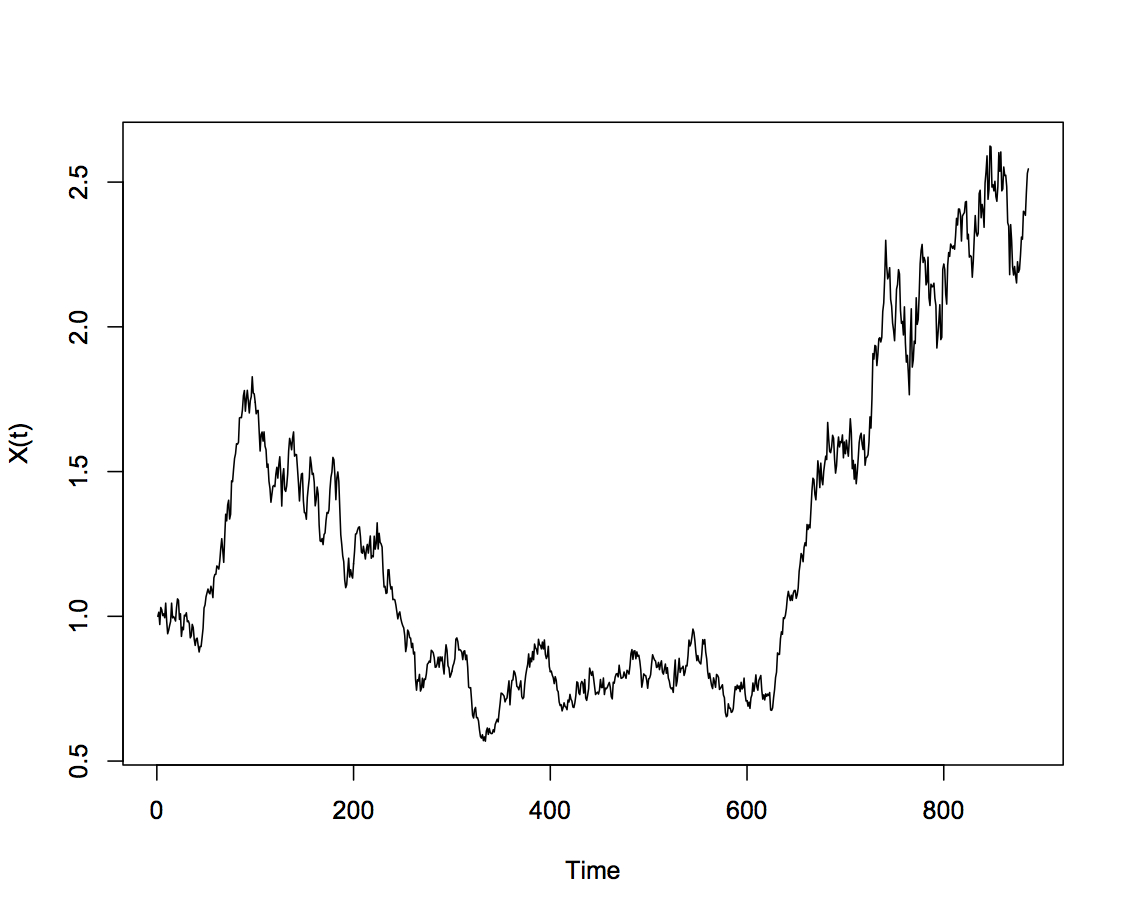
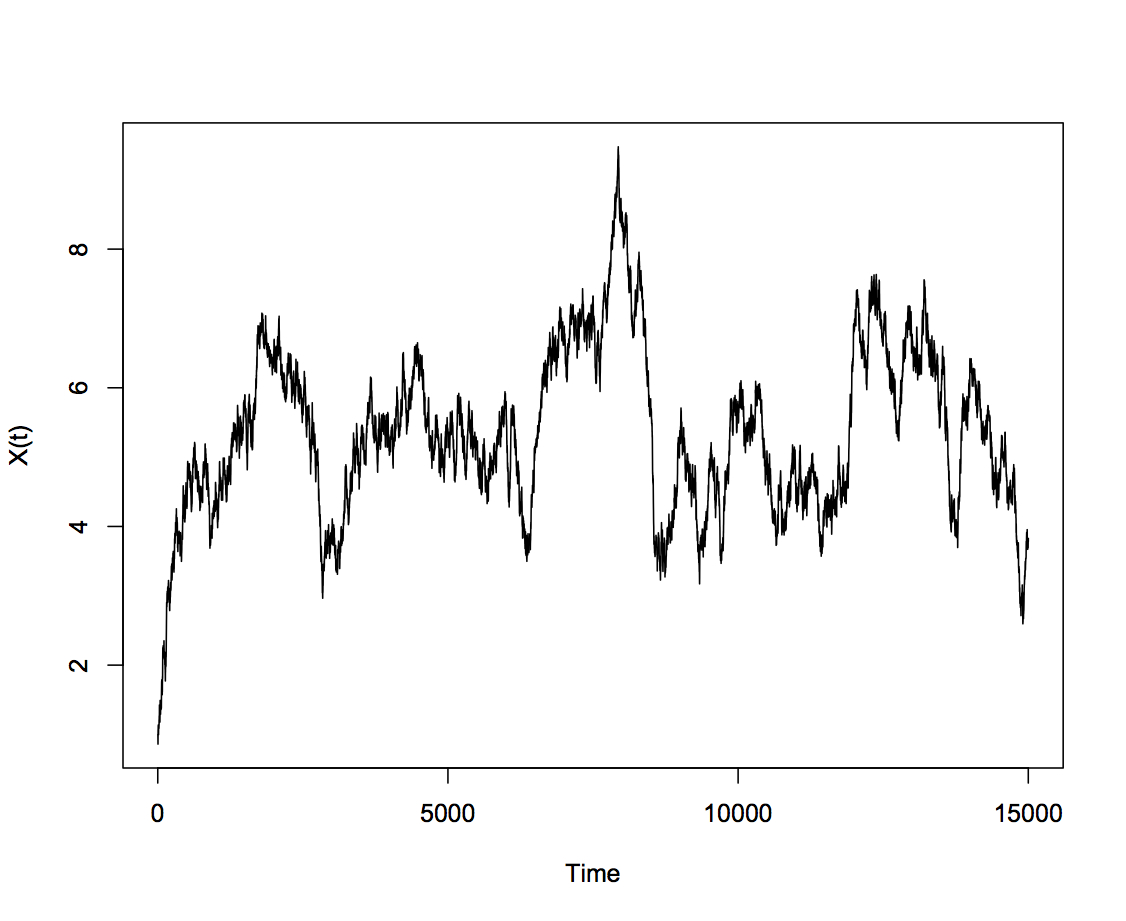
Diffusion processes arise in many places in the physical and economic sciences, for instance as models for stock prices, interest rates, cell movement and paths of molecular particles. Diffusion processes are characterised by several properties, heuristically they are random processes for which their future movement depends only on their current position. The most important property though, for use in modelling physical phenomena, is that the sample paths must be continuous functions of time almost everywhere.
There are many different types of diffusion processes, the best known being Brownian Motion, used to model particle movement and stock prices. In my project I focused on three different processes, Brownian Motion with Drift, Geometric Brownian Motion and the Ornstein-Uhlenbeck Process.
There are two parameters that completely determine a diffusion process, their drift, and their diffusion. My project focused around creating estimators for these two parameters if they are unknown.
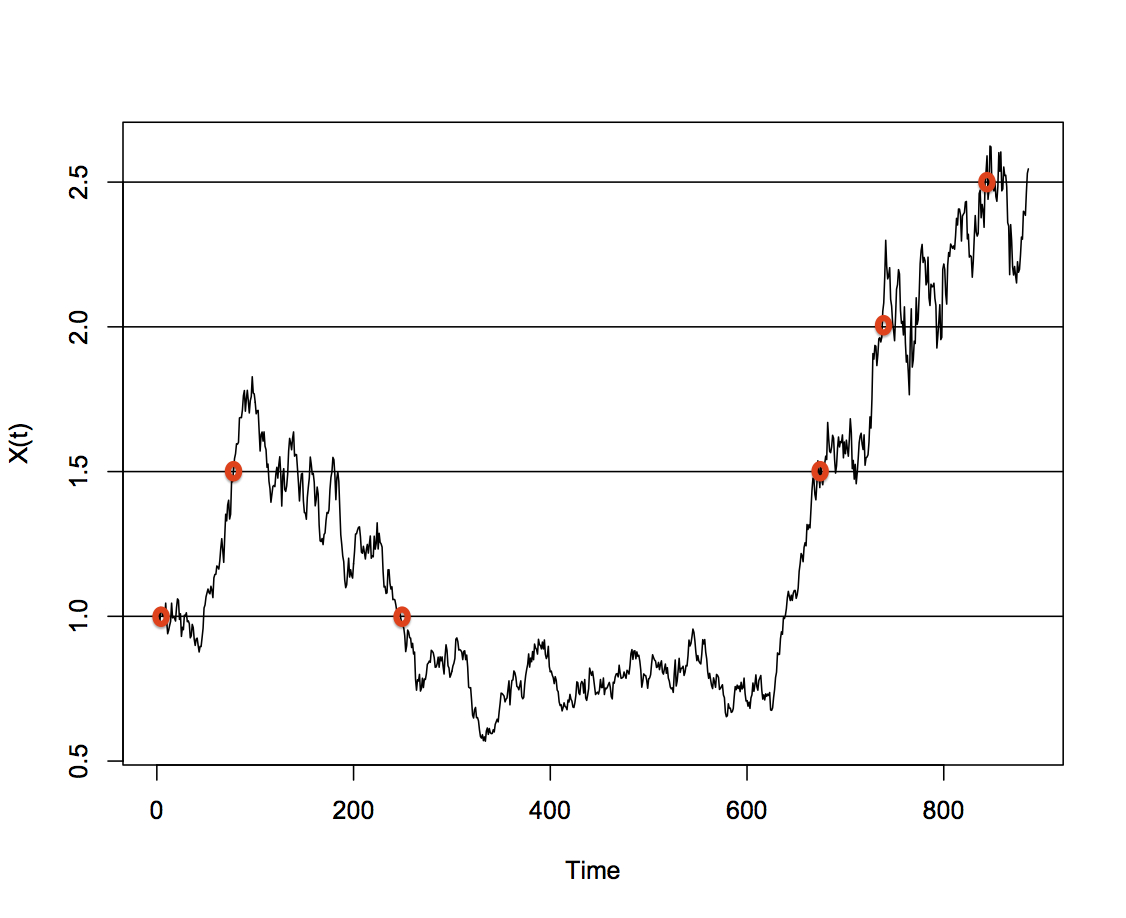
To do this, we made use of an idea called a crossing tree, which is a lattice on which we observe the stochastic process. We take note of the “crossings”of the process, points at which the process intersect either the line above, or below, the previous crossing. If we keep a tally of how many crossings were “up-crossings”, we can derive an estimate of the probability that the stochastic process will step up at any point in time. We can compare this with theoretical probabilities of an up-crossing in order to estimate the parameters of the process.
The second approach taken was to sample the values of the process at regular points in time, similar to how we can take the value of a stock at daily intervals. Specifically, we looked at the time it took for the process to reach a particular level. Once again we derived the theoretical time, and then used this to estimate the parameters of the process.
Lastly, we attempted to combine the two approaches using a technique called Generalised Method of Moments, specifically to attempt to estimate the parameters of the Ornstein-Uhlenbeck process. This was a more difficult task, as it required derivation of “moment conditions”for the time taken for an Ornstein-Uhlenbeck to cross a line, however this required a solution to an integral equation that has not yet been solved analytically. This is a good area for further work on this project, with numerical solutions, or an adapted approach possibly yielding better results.