By Ho Ka Ng, The University of Adelaide
Is the coffee mug the same as the doughnut? This might sound like a silly question but in topology – a branch of mathematics they are considered to be the same. Imagine that a coffee mug made of clay, you can always reshape it to the doughnut without tearing. This is what we mean when two objects are the same. Although this is an initiative definition, it is not practical and sometimes impossible to preform. Instead, we just want to compare some properties of the objects and draw a conclusion. The property that motivated me is called the fundamental group.
What is the fundamental group? Roughly speaking: it is the collection of loops on an object. Suppose we are driving up a steep hill, we obviously cannot drive straight upward. Instead, we can only drive along the spiral. If the hill has a finite height, we will eventually reach the top. However, it turns out that the hill has infinite height and we just looped around it infinitely many times! Now we realise that the hill with infinite height is definitely different to the flat plane. Not only because the hill exists, but also the loops that we drove around. Therefore, to compare two objects, we examine their loops to see if they are different.
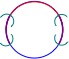
Nonetheless, the fundamental group has a problem. In the depths of mathematics, there is a theorem called the Seifert-van Kampen theorem, which is named after Herbert Seifert and Egbert van Kampen. It states that if we can break up an object into a smaller object, one such that the intersection is in one piece. Then we can find the loops on that object using the loops on the smaller object. It is a crucial tool to calculate the fundamental group of complicated objects, like a double torus. Unfortunately, we cannot use this theorem on a circle. As whenever we break it up into line segments, the intersection is not in one piece, as shown in Figure 1.
Figure 1: The purple bit is not in one piece.
To solve this problem, we look at a similar property of the objects, called the fundamental groupoid. Instead of loops, we are interested in the paths on an object. The paths do a better job at describing the objects since they don’t need to be fixed. In my project, we studied the fundamental groupoid and a generalization of Seifert-van Kampen theorem that used paths. Then we use this theorem to calculate the fundamental group of a circle. The goal is to apply fundamental groupoid to objects with higher dimension as well as develop the Seifert-van Kampen theorem that suits it.
Ho Ka Ng was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.