By Zhigen Lin
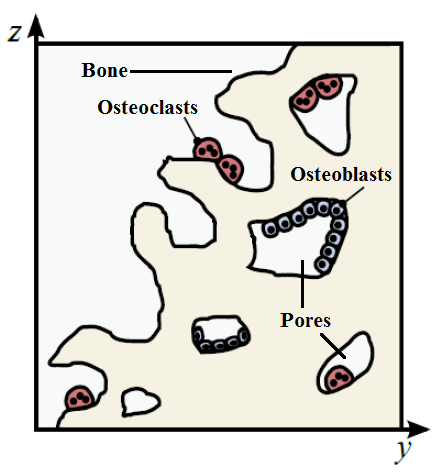
Bones appear to be a hard substance in our bodies that make up our skeleton. They don’t seem to change much after our teenage years. Actually, bone is a dynamic tissue that is constantly being destroyed and reformed in a process known as bone remodelling. There are two main cells involved in this process – osteoblasts, the cells that create bone, and osteoclasts, the cells that remove bone.
Bone needs to be strong in order to protect our organs, but it also must be lightweight, in order to support our movement. For people who have to travel long distances in their daily lives, excessive bone will just weigh them down. For this reason the human body can increase or decrease the amount of bone according to factors such as mechanical load (how much weight we put on it).
So why should we create a mathematical model? One important reason for such a model is that bone formation is affected by resorption (removal) and vice versa, i.e. the two processes are not independent. More technically, we say that formation is ‘coupled’ to resorption. Coupling is the result of a combination of various factors that affect the cells, which is difficult to understand without a model.
In particular, we are interested in how the cell populations and the volume of bone changes over time. To factor in the time component, we use a special class of equations, known as differential equations.
In our model, we used three differential equations to describe bone at a millimetre scale. The variables we are concerned with are osteoblast populations, osteoclast populations and the bone volume fraction (the fraction of bone in a particular millimetre-sized volume, which ranges from 0 to 1).
In order to determine what to include in these equations, we simply require some logical thinking. We can ask ourselves: “What changes the population of a species over time?” It is clear that the populations of cells over time are governed by a birth/source term minus a death/sink term. The amount of bone over time is influenced by the populations of osteoblasts and osteoclasts, the speed at which they act and, more subtly, where they exist (in the holes or pores of the bone!). Some biological and mathematical intuition allows us to derive the three differential equations.
With the groundwork set up, the next steps will be to analyse how stable this system of equations is. One reason the stability is important is because we are looking at a system where the variables are coupled. Once we confirm the stability properties, we can integrate experimental and observed factors such as the typical amount of surface area in bone, the way bone reacts to mechanical load and other mechanical factors.
The big picture goal will be to create a model that enhances our understanding of the bone remodelling process and provides insight into various bone conditions such as osteoporosis. This research could assist in treatment of these conditions in future.
Zhigen Lin was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.