By Helen Hunt
I love Sudoku! I find few things nicer than sitting down with a coffee and a trivial little puzzle. Interestingly, Sudoku belongs to a class of mathematical objects known as Latin squares. Latin squares are square grids in which one object appears exactly once in every row and every column and we’ve known for quite some time that these objects are far from trivial! I would like to explain to you how these objects are so much more useful than simply a way to relax.
For some time, statisticians have used sets of Latin squares to vastly reduce the number of times you need to run an experiment with many different variables.
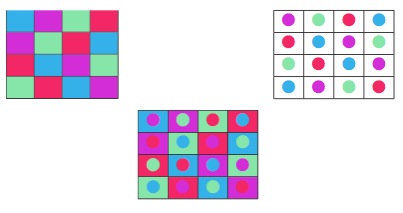
To give you just one example of a way in which they can this, I’m going to talk about mutually orthogonal Latin squares. Firstly, orthogonal means that if you take two orthogonal Latin squares and put one on top of the other, each element of the set of ordered symbols occurs once. Here (figure 1) we see four orthogonal Latin squares that are pairwise (or mutually) orthogonal!
One way orthogonal Latin squares can be used to make our lives easier is to use them to design smart, simple experimental designs. To give an example of how these objects can be used to simplify experiments, let’s say we were to have 4 drugs and 5 doses of each drug that we want to test. We can consider each of our squares above one of these drugs and each symbol in each square a dose of that drug. Then, if we mash them all together as shown in figure 2, we have 25 cells in which each pairwise combination of every drug and dose choice occurs. So, instead of testing each possible combination of drug doses, that is, 625 combinations, we only have to test 25 combinations! You can imagine the implications are even greater when we have larger experimental designs.
Unfortunately – and though it may feel like it – there are not infinite ways to make sets of Latin squares with these properties. In fact, in some cases, we have very few indeed! So that we can still use these sets in the experiments we want to conduct, we have to modify the rules. That’s where what I was looking at over my AMSI vacation research scholarship comes in. I looked at the properties of sets of mutually nearly orthogonal Latin squares. Figure 3 shows an example of these objects.
I tried to find answers to such questions as “What must a set possess numerically to have this property?”. Although I found some interesting answers, my questions are still partially unresolved. We’ve still got a lot to learn!
I would like to express my gratitude to my supervisor, Dr Diane Donovan for her invaluable support and wisdom. Furthermore, the generous support of AMSI made my project possible and I would also like to express thanks to AMSI and CSIRO for organising the Big Day In.
Helen Hunt was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.