By Mehrnaz Noori
Atherosclerosis is a common form of cardiovascular disease that primarily affects large and medium sized arteries. It is the underlying cause of most cases of heart attack, stroke, and vascular dementia and is found in 80 – 90% of people over the age of 30. Fat, cholesterol, calcium, and other substances form plaque, which builds up in arteries and narrows, the passage that blood flows through. This causes arteries to become hard and inflexible which is the leading cause of death in people over 45 and places a significant financial strain on health care systems.
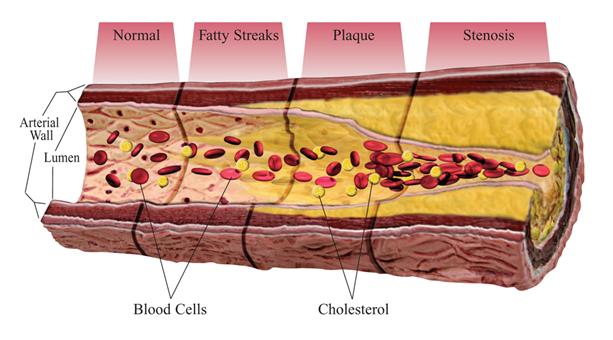
It has been observed that the localization of atherosclerosis may be due to high concentrations of atherogenic substances such as LDL (low-density lipoprotein) in the artery wall and plays a key role in the development of atherosclerosis. In this project we tried to better understand the field distributions of LDL particulate deposition around atherosclerotic lesions.
Presence of an obstacle in the flow would influence the behaviour of the local fluid and would greatly influence either the initiation of an atherosclerotic lesion or the subsequent growth of an existing one.
As depicted in the above figure, the variation of wall shear stress caused by the obstacle will cause a subsequent variation in particulate concentrations. Therefore, the size of the obstacle becomes an essential parameter in the mechanics of the system.
The question may be asked: how can mathematics help to understand this?
For me, as a mathematics student who has been working in computer technology for years, this problem was very interesting and exciting due to its link within mathematical and biological sciences.
Atherosclerosis has been of exceptional interest to me as my mother has suffered from this disease for many years; I would not have thought that one day I might be able to contribute help towards the improvement of this huge burden on human life.
Not many people know that the application of mathematics in biology provides a wealth of opportunities for mathematical modellers.
In this project we firstly worked at understanding the physics of the problem and, secondly, developed the model describing the problem. This was followed by a parametric study of the underlying variables in the system.
The flow behaviour is modelled by coupling the governing Navier-Stokes equations with particle-concentration transport equations. These were then solved on a computational grid, with the appropriate boundary conditions applied.
Using a range of system parameter combinations and the corresponding system results, has given us the opportunity to reach conclusions on the behaviour of the system. We were also able test our ideas to investigate situations that are not easily amenable to experiment. Therefore, this is where mathematics is essential why it is so valuable in this study of the human body.
This project is part of ongoing research on the mechanisms governing atherosclerotic plaque progression and rupture. The methodology and general outcomes may also be employed in the assessment of platelet transport and deposition, as applied to the formation of thrombi in arteries.
Mehrnaz Noori was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.