By Michelle Strumila, Monash University
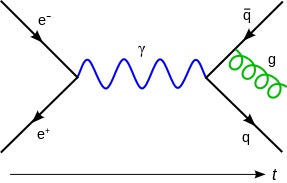
In physics, there is something called a Feynman diagram. It is a way of representing the interactions between particles. This is the way quantum field theory is studied. But then mathematicians came along and decided they didn’t like the vertices, so they smoothed it out and decided on some axioms which best represented what was happening in the physics. Thus was born Topological Quantum Field Theory (TQFT).
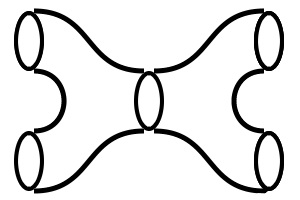In a Feynman diagram, there are lines joined together in some sort of pattern. The centre represents the interactions and the points on the outside represent the particles. A TQFT takes cobordisms, the name given to shapes like the one to the left, and says that the centre represents some sort of function or map, and the outside points represent vector spaces. In some ways these vector spaces are like particles.
These days, there are computers infecting everything we do, they permeate our whole culture and society. But how do they work? Logic. Computers use binary arithmetic, 1’s and 0’s, along with logic gates to process information.
We would like to somehow represent logic gates pictorially.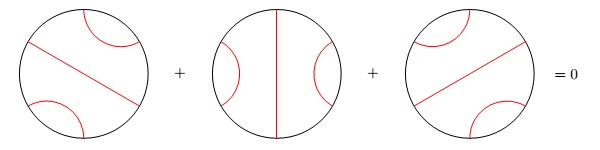
There is a relation called the Bypass Relation, which involves these three discs. It would be nice if they represented the values “True”, “False” and maybe some sort of indeterminate. In a similar way to cobordisms in a TQFT, what if our “particles” are these values, and our cobordism is the gate? This can be represented in two ways: a “pair of pants” or a disc with two holes. By having the lines join up different points, perhaps we can form different logic gates.
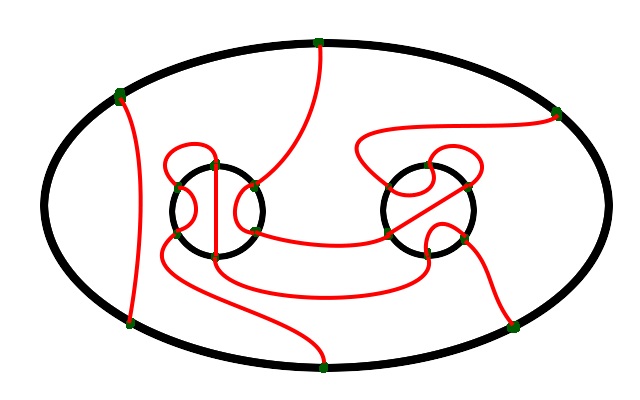
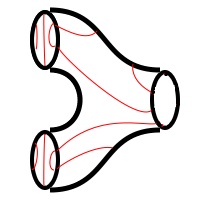So, can lines be drawn such that the two holed annulus is some sort of logic gate? Can an annulus form a NOT gate? Actually, it turns out the answer is no. Still, it would be nice to represent logic gates topologically, even if this avenue did not work out. It is something for future mathematicians to think about.
Michelle Strumila was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.