Christopher Ryba, The University of Sydney
Over the course of the summer, I undertook an AMSI Vacation Research Scholarship. Under the supervision of Prof. G. I. Lehrer, I studied the representation theory of Temperley-Lieb algebras.
Representation theory can be thought of as the study of how algebraic structures arise in linear spaces. The main focus is on the properties of representations of a given structure with matrices. This framework turns out to be indispensable in particle physics, as well as in statistical mechanics (where the Temperley-Lieb algebras appear in some models for magnetism).
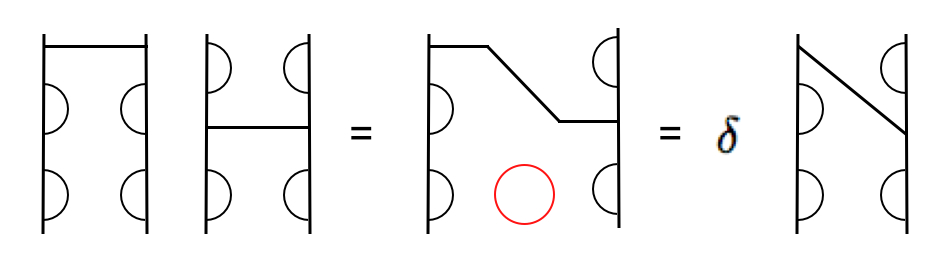
The Temperley-Lieb algebras, which I was learning about, appear in many different contexts. One approach is via the theory of quantum groups; this has intimate connections to other areas such as the theory of braid groups (which have appeared in exciting recent developments in quantum computing). Another approach comes from the perspective of diagram algebras, which easily demonstrate the intricate structure of the algebras. The Temperley-Lieb algebras can be understood in terms of diagrams of non intersecting lines connecting a collection of points. These can be multiplied, just by placing the diagrams end to end (for every internal loop that occurs in this process, the result is multiplied by a certain number, delta).
In fact, the Temperley-Lieb algebras belong to a class of algebras called Cellular Algebras, which have a well developed theory. This allows the study of their properties in terms of modifications of the diagrams mentioned previously. By considering the combinatorics of how certain “tableaux” (consisting of a row of points, some of which are connected by nonintersecting arcs) combine, it is possible to obtain structural information about the algebra (such as about whether or not it satisfies a property called semisimplicity). This leads to an interesting interplay between combinatorics and the representation theory of quantum groups. Such connections have had a substantial influence in some aspects of representation theory, as well as in applications.
Christopher Ryba was one of the recipients of a 2013/14 AMSI Vacation Research Scholarship.